È possibile rappresentare una matrice attraverso un grafo?
Prima di concentrarmi sulla domanda presente nel titolo, vorrei fare una premessa.
Qualche tempo fa, grazie al blog del Prof. Riccardo Rigon - professore ordinario presso il Dipartimento di Ingegneria Civile, Ambientale e Meccanica di Trento, sono venuto a conoscenza di Math3ma.
Mat3ma nasce nel 2015 dall’idea di Tai-Danae Bradley, una dottoranda in matematica presso il City University of New York, che si occupa principalmente di fisica quantistica e teorica.
Come dottore in ingegneria (anche se mi fa strano dirlo :D) posso affermare che, nonostante mastichi abbastanza bene la matematica, quest’ultima viene utilizzata dagli ingegneri principalmente come mezzo per arrivare ad una soluzione (talvolta) soddisfacente. Questo fatto fa si che veniamo spesso derisi da fisici e matematici, in quanto “ignoranti” nella materia più sofisticata del mondo.
Ma non è questo l’argomento che voglio trattare quest’oggi.
Ma che cosa è un grafo?
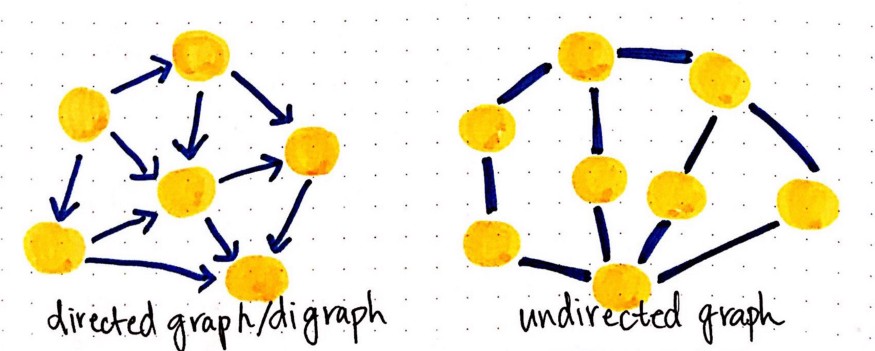
Tipologie di grafo | Fonte: medium.com
Un grafo è un insieme di n nodi tra loro connessi da t tratti (o archi) che possono essere orientati (descritti da una direzione e un verso) o non orientati (di verso arbitrario).
Un grafo si differenzia da un “albero” (tree) principalmente perché quest’ultimo è definito da un verso; mi spiego meglio: in un albero, ogni vertice ha un nodo precedente e un nodo successivo che ne definiscono il verso. Inoltre, ogni nodo può avere solamente un nodo, passatemi il termine, “padre” (o genitore). Esiste quindi uno e uno solo nodo di partenza (root); esiste, quindi, una gerarchia per i nodi. Questo non accade in un grafo, che per come è definito non ha alcun nodo root.
Elemento che lega le due tipologie appena descritte è il numero di nodi: infatti, un grafo - per essere tale - deve essere formato da almeno un nodo, come un albero deve avere come minimo un vertice iniziale.
Formalmente, un grafo è una coppia ordinata $$ G = (V, E) $$
dove \(V\) è l’insieme di nodi (o vertices) $$ V = \{v_1, v_2, \dots, v_n\} $$ e \(E\) è l’insieme dei tratti (edges o links) $$ E = \{e_1, e_2, \dots, e_t\} $$
Come si può vedere nelle figure seguenti, la differenza tra un grafo non ordinato e uno ordinato è sostanziale.

Esempio di grafo non ordinato

Esempio di grafo ordinato
Infatti, il k-esimo tratto che congiunge i nodi \(i\) e \(j\), per un grafo ordinato, viene scritto come \(e_k = (v_i, v_j),~i\neq j\).
Alcune curiosità sulla teoria dei grafi
La teoria dei grafi vede la luce per la prima volta nel 1736, grazie a Eulero. Il matematico svizzero, infatti, risolse il problema dei sette ponti di Königsberg utilizzando quella che sarebbe poi diventata la teoria dei grafi. Eulero si chiedeva se fosse possibile partire e arrivare nello stesso punto della città attraversando tutti i ponti una sola volta.
Grazie alle basi poste da Eulero, la teoria dei grafi si è evoluta ed è tutt’ora impiegata nella descrizione e nella risoluzione di reti di acquedotti o in algoritmi per il calcolo del percorso (chiuso) più breve tra tutte le città del mondo (più info sulla soluzione potete trovarle qui).
La teoria dei grafi è - come ogni teoria matematica - descritta da teoremi che non esporrò, per non tediarvi con argomentazioni facilmente reperibili altrove.
è possibile rappresentare una matrice attraverso un grafo?
La risposta è:
sì, si può!
Ma quindi?
Il titolo descrive alla perfezione ciò che è presente nelle righe che seguono: è possibile rappresentare una matrice attraverso un grafo?”
La risposta è “sì, si può!”
E non solo: è anche possibile derivare una matrice da un grafo.
L’idea di Tai-Danae Bradley è che ogni matrice può essere rappresentata da un grafo pesato “bipartito”. Per pesato si intende che ad ogni tratto corrisponde una valore; mentre, un grafo bipartito (detto anche bigraph) è un grafo i cui nodi possono essere suddivisi in due insiemi differenti (e.g. \(\mathbb{U}\) e \(\mathbb{V}\)) rappresentati con colori diversi.

Per un grafo bipartito, allora vale $$ G = (U, V, E) $$
Ad esempio, per il seguente grafo corrisponde la matrice alla sua sinistra.

Le righe della matrice corrispondono ai tre nodi verdi del grafo, mentre le due colonne sono rappresentate dai nodi rossi sulla destra.
Il valore del lato è così calcolato: si consideri ad esempio l’elemento \(M_{11}\) della matrice \(\underline{\underline{M}}\); l’elemento si trova sulla riga \(1\) e sulla colonna \(1\), cioè collega il primo nodo a sinistra (riga \(1\)) con il primo nodo a destra (colonna \(1\)). Il valore del lato è, appunto \(-1\).
Proseguendo, considerando l’elemento \(M_{21}\) - che è posizionato sulla riga \(2\) e sulla colonna \(1\) e collega il secondo nodo verde con il primo nodo rosso. L’etichetta del tratto considerato è il valore corrispondente a \(M_{21}\) (i.e. \(4\)).
Al contrario, i valori nulli della matrice \(\underline{\underline{M}}\) significano che non sono presenti tratti che congiungono i nodi in esame.
Formalmente, una matrice può essere anche vista come una funzione che prende valori da degli insiemi \(\mathbf{X}\) e \(\mathbf{Y}\) e riporta valori in \(\mathbb{R}\)
Ma perché è possibile questo?
Formalmente, una matrice \(\underline{\underline{M}}\) è un “array” di dimensioni \(n \times m\), ma può essere anche vista come una funzione che prende valori da degli insiemi \(X\) e \(Y\) e riporta valori in \(\mathbb{R}\) $$ M: X\times Y \longrightarrow \mathbb{R} $$
ove $$ X = \{x_1, x_2, \dots, x_n\}~,~ \quad Y = \{y_1, y_2, \dots, y_m\} $$
Allora, l’elemento \(M_{ij}\) può essere rappresentato come
$$ M_{ij} = M(x_i, y_i) , \quad \forall i \in 1, 2, \dots, n~,\quad\forall j = 1, 2, \dots, m $$ La seguente immagine riassume quanto appena scritto.

E questo è tutto per quanto rigurda la rappresentazione di una matrice come grafo.
Prodotto tra matrici
I medesimi concetti possono essere applicati al prodotto tra matrici, che corrisponde a percorrere tutti i possibili percorsi che collegano i due nodi.
Si comprende meglio analizzando la seguente figura:

Nella figura sono presenti due matrici: \(\underline{\underline{M}}\) e \(\underline{\underline{N}}\) tali che
$$ M: X \times Y \longrightarrow \mathbb{R}~,\quad N: Y \times Z \longrightarrow \mathbb{R} $$
dove in questo caso si ha \(X = \{x_1, x_2, \dots, x_n\}\) e \(Z = \{z_1, z_2, \dots, z_l\}\), essendo i nodi \(\{y1, y2, \dots, y_m\}\) nodi interni e quindi non ricadenti nel prodotto.
Come ben sapete, il prodotto tra due matrici è un prodotto riga per colonna perciò, il numero di colonne di \(\underline{\underline{M}}\) deve corrispondere al numero di righe di \(\underline{\underline{N}}\). Guardando la figura sopra riportata si può notare che così è.
Secondo quanto detto sopra, il primo elemento della matrice prodotto - cioè risultante dal prodotto \(\underline{\underline{M}}\,\underline{\underline{N}}\) - è definito come l’etichetta del tratto che congiunge i due nodi \(x_1\) e \(z_1\) (vale, quindi, anche l’opposto di quanto detto sopra). Ma in questo caso, i tratti che congiungono i nodi sono molteplici; allora, il valore finale dell’elemento è definito come la somma dei prodotti delle etichette sui lati per ogni percorso; Per il primo elemento si trovano i percorsi \(\overline{(x_1\,y_1\,z_1)}\) e \(\overline{(x_1\,y_2\,z_1)}\), dove
$$
\begin{aligned}
&\overline{x_1\,y_1} = -1\quad &&\overline{y_1\,z_1} = 5
&\overline{x_1\,y_2} = 2 \quad &&\overline{y_2\,z_1} = -7
\end{aligned}
$$
Moltiplicando i termini dei singoli percorsi si ottiene $$ \overline{(x_1\,y_1\,z_1)} = -1\cdot 5 = -5 \quad \overline{(x_1\,y_2\,z_1)} = 2\cdot -7 = -14 $$
L’elemento \((M\,N)_{11}\) è la somma dei prodotti appena calcolati, cioè
$$
(M\,N)_{11} = -5 - 14 = -19
$$
che corrisponde al valore dell’elemento sulla prima riga e sulla prima colonna della matrice prodotto e quindi al valore del tratto che collega \(x_1\) a \(z_1\).
Come si può notare dal grafo a destra, nel grafo risultante i nodi interni \(Y\) collassano, ottenendo effettivamente il grafo che corrisponde a una matrice di dimensioni \(3 \times 2\).
Altre applicazioni
L’autore prosegue la trattazione descrivendo, ad esempio, le matrici simmetriche e trasposte e i relativi grafi, nonché applicando la teoria descritta ad elementi di probabilità che io non discuterò.
Vi invito comunque a visitare il suo blog per trovare spunti riflessivi particolarmente interessanti ed ampliare le vostre conoscenze matematiche.
- "Viewing Matrices & Probability as Graphs" (Math3ma.com)
- "A Gentle Introduction To Graph Theory" (medium.com)
- "Teoria dei grafi e applicazioni" (science.unitn.it)
- "Bipartite graph" (wikipedia.org)